Préambule

Dans ces deux cas, les personnes font du commerce : de viennoiseries à gauche et d’immobilier à droite. Par contre, leurs attitudes divergent :
- la confiance est installée à gauche : ils peuvent faire du commerce sans se poser de questions : la monnaie joue son rôle de référentiel, personne n’a de doutes sur ce qu’il pourra faire des billets et pièces en sortant du magasin. C’est ainsi qu’on comprend que la valeur d’une monnaie est basée sur la confiance qu’on a en elle > tout le monde est d’accord sur le fait que ce billet vaut 10 €
- à droite ils n’ont d’autre choix que de lire et relire avant de signer : ils n’ont pas de référentiel commun, n’ont pas de tiers de confiance qui leur garantisse un contenu
Pourquoi a-t-on besoin d’un tiers ? Parce que leurs intérêts ne sont pas convergents, la confiance ne peut s’installer. Ce sujet, qui relève bien sûr des sciences humaines et sociales, a été historiquement traité par la présence d’un tiers de confiance, physique (un notaire) ou matériel (une monnaie fiduciaire)
Il a aussi été traité par les mathématiques et l’informatique. Voyons comment.
Ces comportements sont-ils modélisables ?
- La théorie des jeux
La théorie des jeux est un domaine des mathématiques qui s’intéresse aux interactions stratégiques. Depuis 1944, 11 prix Nobel ont été décernés à des économistes et mathématiciens pour leurs recherches sur cet environnement. Vers 1950, John Forbes Nash formalise une notion générale d’équilibre qui portera le nom d’équilibre de Nash
Le concept se décrit comme suit : Avec un complice, vous êtes emprisonné pour avoir monté une escroquerie. Vous êtes interrogés séparément et avez le choix d’avouer ou de nier.
Les règles sont inscrites ci-dessous :
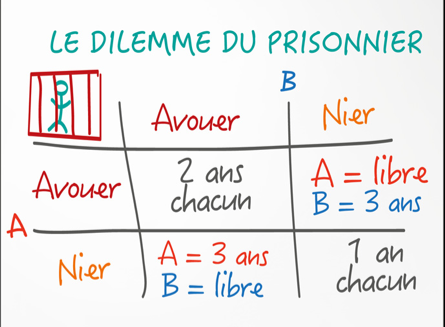
Le paradoxe est là : la solution toute indiquée par un raisonnement cartésien mène à une situation qui n’est pas la meilleure pour les deux joueurs.
La théorie des jeux trouve de nombreuses applications : politique (pensez à la guerre froide), économique (implantation commerciale/date de sortie d’un produit, guerre des prix ou entente), en management (que vont penser les autres si je promeus untel ? Dominer l’autre me mènera-t-il à des gains à terme) et, nous y viendrons plus tard, en informatique.
Pour le dire (trop) simplement, la théorie des jeux permet de mieux comprendre les interactions sociales.
Si vous avez la curiosité d’aller un peu plus loin, je vous conseille ce lien : https://ayowel.github.io/trust/, c’est ludique et complet.
2. Le problème des généraux byzantins
Le concept est vulgarisé ainsi : il décrit la manière dont un groupe de généraux encerclant une citadelle doit s’accorder sur une stratégie commune.


Ce concept mathématique est destiné à concevoir des modèles aptes à continuer à fonctionner même si l’un des composants de fonctionne plus. Il est couramment utilisé pour les systèmes informatiques. Dans ces métiers, les pannes sont dites byzantines quand le système donne des résultats aléatoires.
Appliqué à des modèles humains, les pannes peuvent être de l’ordre du retrait ou de la malveillance.
L’application à la blockchain
Associées à la cryptographie, la théorie des jeux et le concept des généraux byzantins permet de sécuriser la blockchain. En effet,
- peut-on concevoir qu’elle ne résiste pas à des pannes aléatoires et dites byzantines ?
- peut-on s’assurer du comportement des acteurs qui ont la charge de sécuriser la blockchain, aussi de ceux qui l’utilisent ?
- Le fonctionnement d’une blockchain
Démêlons ensemble une définition communément exprimée ainsi : il s’agit d’un protocole distribué qui est sécurisé par un modèle dit « proof of work ». Fabriquons ensemble et de manière imagée une blockchain :
Je vais transmettre un fichier par mail à 10 d’entre vous. En l’état, rien ne vous empêche de le modifier. Nous allons donc nous fixer 3 règles (c’est le « protocole », imaginons que nous le signions) :
- Le fichier original sera celui qui est majoritaire parmi nous
- Nos ordinateurs seront reliés les uns aux autres, s’interrogeront pour savoir si l’un d’entre nous n’a pas modifié une donnée
- Celui d’entre nous qui aura un fichier différent le verra remplacé par celui qui est majoritaire
Voilà, c’est tout. Cherchez la faille de ce modèle ! Pour autant que notre blockchain soit étendue, nous avons là un système sécurisé. L’est-il à 100%, pas encore. On ne peut exclure l’infidélité d’une majorité des acteurs. Ajoutons-y la « proof of work », appelons-là preuve de travail (il existe aussi la preuve d’enjeu (nous y reviendrons dans un autre article) :
Les 10 acteurs ci-dessus sont dénommés des « mineurs » (en référence aux chercheurs d’or). Par protocole, ils ont les devoirs et les droits suivants :
- Vous stockerez la blockchain sur votre serveur (il y a donc dans notre exemple 10 blockchain identiques)
- En contrepartie de cette tâche, il vous sera soumis toutes les 10 mn un calcul d’une extrême complexité (ça ressemble à un Sudoku – c’est très difficile à faire, mais facile à vérifier). Le 1er d’entre vous qui trouvera le résultat sera rémunéré en bitcoin.
Puisque le calcul est d’une grande complexité, les mineurs doivent investir dans du matériel extrêmement puissant, et donc très cher. C’est cet investissement qui les rend fidèles :
- Peut-on imaginer que, ne serait-ce l’un d’entre eux ne joue pas le jeu du protocole ? Probablement pas, il serait exclu et risquerait de perdre son métier.
- Peut-on imaginer qu’une majorité parmi des milliers de mineurs ne joue pas le jeu ? Evidemment non.
- Peut-on imaginer que l’un d’entre eux investisse jusqu’à devenir majoritaire et puisse ainsi voler des bitcoin ? Non, bien sûr (au-delà du coût d’une telle attaques- environ 15 Md $ à ce jour) il s’exposerait à ce qu’il vient de voler perde immédiatement sa valeur (souvenons-nous qu’une monnaie ne vaut que par la confiance qu’on a en elle).
En forçant le trait, on saurait dire que c’est l’instinct de préservation et/ou la cupidité qui rend les mineurs fidèles au protocole.
2. Les acteurs extérieurs
Sur des critères comportementaux, les utilisateurs que nous sommes ne sont bien sûr pas différents des mineurs. Nous avons vu le fonctionnement d’une blockchain. Elle trouve bien sûr d’autres usages que les crypto-monnaies, et peut servir de machine à preuve. Elle sait en effet dire de manière infaillible :
- tel jour, telle heure, ce document était à tel état
Seule, elle donnera tout de même des preuves juridiquement (très) imparfaites : si vous faites un faux et que vous le mettez dans une blockchain, il sera certes certifié, mais il restera faux (cf https://www.contractchain.io/la-blockchain-et-le-droit-de-la-preuve/)
ContractChain répond à cette unique faille : quand vous proposez une documentation contractuelle à votre contradicteur (n’hésitons pas à utiliser ce mot, puisque vos intérêts divergent), elle est nécessairement ancrée dans la blockchain (le fameux référentiel commun) et est soumise à vos approbations : si vous l’approuvez et que vous la signez, alors l’accord sera parfait.
Synthèse
Nous avons vu ci-dessus comment modéliser des comportements, et tenir compte de ceux-ci pour fabriquer un modèle solide.
Nous nous sommes aussi décrits comme étant (parfois) méfiants et malicieux, cupides ou plus simplement cherchant à nous préserver. Dans des relations commerciales, décrivons-nous plus simplement comme ayant des intérêts divergents.
Puisque celui qui triche (mineur ou utilisateur) sera certain de se faire prendre la main dans le pot de confiture, la blockchain, accompagnée de ContractChain pour une revue documentaire, ne saurait-elle agir en « tiers auquel on peut faire confiance », pour que cette dernière soit implicite
Et donc,
Ne serait-on pas capables de rendre nos relations plus vertueuses ?
christophe@contractchain.io
Bibliographie
- http://renaud.bourles.perso.centrale-marseille.fr/Cours/Theorie_des_jeux.pdf
- https://www.cairn.info/revue-vie-et-sciences-de-l-entreprise-2005-3-page-6.htm#
- https://www.institut-pandore.com/economie/comprendre-theorie-des-jeux/
- https://fr.qwe.wiki/wiki/Byzantine_fault_tolerance
- https://www.binance.vision/fr/blockchain/byzantine-fault-tolerance-explained